










untergeordnete
Seiten:
|
Physik, 12 - mechanische
Schwingungen und Wellen - Achtung:
lange Ladezeit !!! |
Übersicht
Es gibt in unserer Umwelt viele
Vorgänge welche in regelmäßigen Zeiten oder räumlichen Abständen gleiche
Bewegungszustände durchlaufen. Schwingungen und Wellen treten in vielen
Teilbereichen er Physik auf. Am anschaulichsten und mathematisch am
einfachsten zu erfassen sind sie am Beispiel der mechanischen Wellen.
Hier der
Link zum Download der aller in dieser Reihe verwendeten Folien:
Sammlung Schwingungen
(Stand 6.6.05)
Außerdem eine
umfangreiches Script zum Thema
Schwingungen, welches ich selber im Netz (keine Ahnung mehr wo)
aufgetrieben habe. Schwingungsvorgänge und
-größen
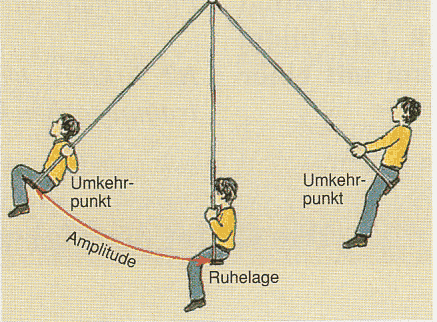 Führt ein Körper periodisch
Hin- und Herbewegungen um eine Ruhelage aus, so nennt man dies eine
Schwingung.
-
Die Bewegung ist
periodisch, wenn sich die Bewegungszustände in gleichen
Zeitabschnitten wiederholen.
-
Klingt
die Schwingung im Laufe der Zeit ab, so spricht man von einer gedämpften
Schwingung, andernfalls handelt es sich um eine ungedämpfte Schwingung.
-
Die Bewegung
verläuft zwischen zwei Umkehrpunkten durch den Ruhepunkt
des schwingenden Teilchens (Oszillators).
|
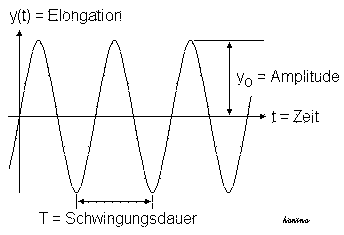 Zur Beschreibung einer Schwingung
dienen folgende Größen:
Die Schwingungsdauer oder
Periodendauer T ist der für eine
vollständige Schwingung benötigte Zeitabschnitt.
Die Frequenz f ist der Quotient aus der Anzahl n der Schwingungen und
der dazu benötigten Zeit t oder dem Kehrwert der Periodendauer T: f=n/t.
Die Einheit der Frequenz ist 1 Hertz:
Die momentane Auslenkung oder
Elongation y(t) (Strecke als
Funktion der der Zeit) gibt den Weg an, um den sich der Oszillator aus
der Ruhelage entfernt hat. Auslenkung nach unterschiedlichen Seiten des
Ruhepunkts unterscheidet man im Vorzeichen.
Die maximale Auslenkung oder die
Amplitude y0 der Schwingung ist
der Betrag der größten Elongation. |
Für die Frequenz ergeben sich folgende Zusammenhänge
Eine vertiefende Behandlung der Schwingungsgrößen findet sich auf der
untergeordneten Seite
Schwingungsgrößen.
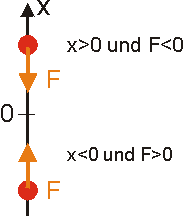 Das
besondere Merkmal aller Schwingungen eine stets zur Ruhelage
gerichtete rücktreibende Kraft. Das
besondere Merkmal aller Schwingungen eine stets zur Ruhelage
gerichtete rücktreibende Kraft.Ist die rücktreibende Kraft
umso größer je größer die Auslenkung ist (lineares Kraftgesetz F ~
x) so kommt es zu einer harmonischen Schwingung.
Umgekehrt kann man aus dem Vorliegen einer harmonischen Schwingung
auf ein lineares Kraftgesetz schließen.
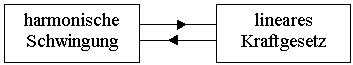 |
harmonische
Schwingung
Der
wichtigste Schwingungstyp ist die harmonische Schwingung oder die
Sinusschwingung. Das heißt, die Amplitude bleibt konstant - die Schwingung
ist ungedämpft. Er tritt z. B. bei der Projektion einer gleichförmigen
Kreisbewegung oder bei der Schwingung eines Feder- oder Schwerependels auf.
Eine genauere Beschreibung der
Projektion von Kreisbewegungen erfolgt auf der untergeordneten Seite
Schwingung - Kreis.
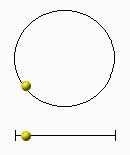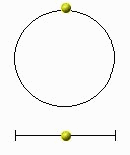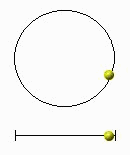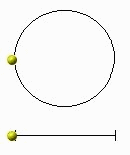 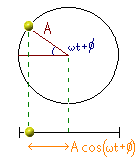 Die Phase
einer Schwingung gibt an, in welchen Abschnitt des sich
wiederholenden Zyklus sich die Schwingung befindet.
Mathematisch ausgedrückt ist die Phase das w in
sin(wt). Die Phase
einer Schwingung gibt an, in welchen Abschnitt des sich
wiederholenden Zyklus sich die Schwingung befindet.
Mathematisch ausgedrückt ist die Phase das w in
sin(wt).
x(t)=x0 sin(wt)
In der Einheit Grad ist ein Zyklus für w = 360° abgeschlossen.
Für viele physikalischen Probleme ist die Phase einer
Schwingung zum Startzeitpunkt irrelevant. Man kann in diesen
Fällen w = 0 annehmen. |
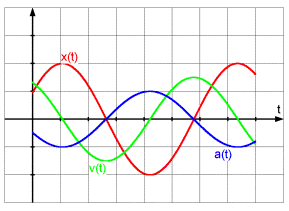 Es
gelten folgende Gesetze: Es
gelten folgende Gesetze:x(t)=x0 sin(wt)
v(t)=x0 w cos(wt)
a(t)=-x0 w² sin(wt)
= -w² x(t)
|
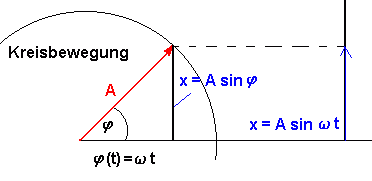 Es
gilt: Es
gilt:x(t)=A sin(wt)
v(t)=A
w cos(wt)
a(t)=-A
w² sin(wt)
Für eine Federschwingung
ergibt sich:
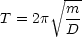
Eine erläuterte
Herleitung findet sich auf der untergeordneten Seite
math. Beschreibung.
Eine Simulation der
Pendel befindet sich auf der untergeordneten Seite
Pendel. |
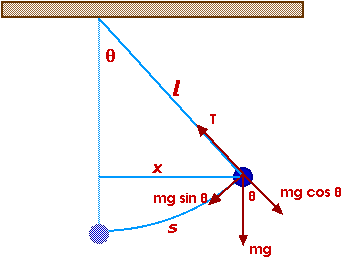 Für eine
Schwerependelschwingung
ergibt sich :
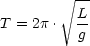
Eine erläuterte
Herleitung findet sich auf der untergeordneten Seite
math. Beschreibung.
Eine Simulation der
Pendel befindet sich auf der untergeordneten Seite
Pendel. |
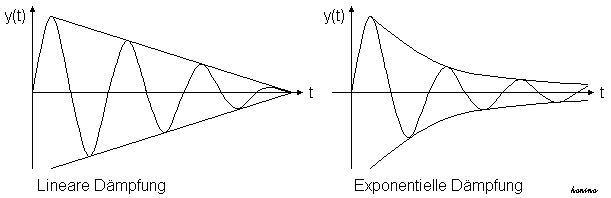
Reale Schwingungen sind immer
gedämpft, da sie, z. B. durch Reibung, immer Energie an die Umgebung
abgeben. Überlässt man ein solches System ohne äußere Energiezufuhr sich
selbst (freie Schwingung), so führen diese Energieverluste zu einer
Verkleinerung der Amplitude und letztendlich zum Stillstand der
Schwingung.
Bei realen Schwingungen ist die
dämpfende Kraft häufig proportional zur Geschwindigkeit. In diesem Fall
nimmt die Amplitude exponentiell ab (A(t)=A0
e-kt ), d.h. die Einhüllende
ist eine Exponentialkurve.
Um die Dämpfung
mathematisch zu beschreiben, muss bei der
mathematischen
Beschreibung des harmonischen Oszillator ein Dämpfungsterm eingefügt
werden: Ein Beispiel für geschwindigkeitsproportionale Reibung ist
die Reibung in einem Fluid (Flüssigkeit oder Gas), etwa ein
Pendel mit Luftreibung. |
| Eine solche gedämpfte harmonische Schwingung lässt sich
beschreiben durch: y(t)=y0
e-kt sin(wt)
(ungedämpft: y(t)=y0sin(wt)) Eine genauere Beschreibung der
Dämpfung mit Simulationen erfolgt auf der untergeordneten Seite
Dämpfung.
|
Interferenz
In vielen Fällen sind an der
Entstehung eines Bewegungsvorgangs mehrere Schwingungen beteiligt, die
sich Additiv überlagern (Interferenz). Das Ergebnis hängt entscheidend von den
Ausbreitungsrichtungen, den Frequenzen der Schwingungen und deren
Phasendifferenz ab.
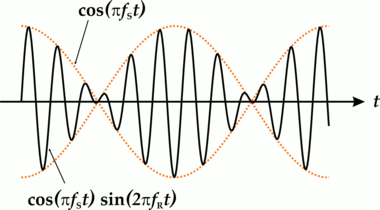
Überlagern sich zwei
Schwingungen, die sich nur geringfügig in ihrer Frequenz unterscheiden kommt
es zu einer Schwebung.
 Dann
kann die Summenschwingung so dargestellt werden: Dann
kann die Summenschwingung so dargestellt werden:
![y_R = \hat{y}[\sin (2\pi f_1t) + \sin(2\pi f_2t)]](ph12_down/910ea8e9dce471fa74234839fd97f232.png) Diese Berechnung kann umgeformt
werden in die folgende Formel:
![y_R = 2\hat{y}\cos [\pi(f_1-f_2)t]\cdot \sin [\pi(f_1+f_2)t]](ph12_down/a116fc00b33d306298e250bf6ea38f50.png)
Die letzte Formel besagt, dass
die Schwebungsfrequenz der mittleren Frequenz von beiden Obertönen
entspricht (das Sinus-Glied der Formel, siehe fR
unten), und dass die resultierende
Amplitude
der Schwebung sich zeitlich ändert (dies wird durch das Kosinus-Glied
ausgedrückt, siehe fS
unten).
Es gilt also:
fS = f1 − f2,
sowie
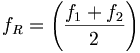 . .
|
Eine genauere Beschreibung der
Interferenz erfolgt auf der untergeordneten Seite
Interferenz.
|
 J.B.Fourier
zeigte Anfang des 19. Jahrhunderts, dass sich periodische Vorgänge
als Summe harmonischer Schwingungen darstellen lassen. Ist die
Periodendauer T bekannt, so hat die erste harmonische Schwingung (Grundschwingung)
die Frequenz f = 1/T. Die weiteren harmonischen Schwingungen (die so
genannten Oberschwingungen) haben ganzzahlige
Vielfache dieser Grundfrequenz. J.B.Fourier
zeigte Anfang des 19. Jahrhunderts, dass sich periodische Vorgänge
als Summe harmonischer Schwingungen darstellen lassen. Ist die
Periodendauer T bekannt, so hat die erste harmonische Schwingung (Grundschwingung)
die Frequenz f = 1/T. Die weiteren harmonischen Schwingungen (die so
genannten Oberschwingungen) haben ganzzahlige
Vielfache dieser Grundfrequenz.
Die Diskrete Fourier Transformation zerlegt ein beliebiges periodisches
Signal in seine Basis-Frequenz-Komponenten (Sinus, Kosinus). |
Eine genauere Beschreibung der
Fourier Analyse mit Simulationen erfolgt auf der untergeordneten Seite
Fourier.
Resonanz
 Resonanz: ist das Anwachsen der Amplitude (Schwingungsweite,
Auslenkung) einer mechanischen oder elektrischen Schwingung,
dadurch, dass eine äußere Kraft das schwingende System
periodisch "im richtigen Takt" anregt. Resonanz: ist das Anwachsen der Amplitude (Schwingungsweite,
Auslenkung) einer mechanischen oder elektrischen Schwingung,
dadurch, dass eine äußere Kraft das schwingende System
periodisch "im richtigen Takt" anregt.
Das funktioniert also nur, wenn sie dies genau mit der
"richtigen" Frequenz, d.h. der Eigenfrequenz des
Systems (oder einem Vielfachen davon) macht.
|
 Eigenfrequenz: ist die Frequenz, mit der ein System frei schwingt. Jedes
System hat dabei ganz bestimmte Eigenfrequenzen. Sie hängen
von den physikalischen Gegebenheiten des Systems (z.B.
Masse, Pendellänge, Federhärte, usw. ab). Eigenfrequenz: ist die Frequenz, mit der ein System frei schwingt. Jedes
System hat dabei ganz bestimmte Eigenfrequenzen. Sie hängen
von den physikalischen Gegebenheiten des Systems (z.B.
Masse, Pendellänge, Federhärte, usw. ab).
Anders gesagt,
alle schwingungsfähigen Systeme haben eine Eigenfrequenz,
und wenn wir es mit dieser Eigenfrequenz zum Schwingen
bringen, kann sich die Schwingung zu riesigen Werten
"aufschaukeln".
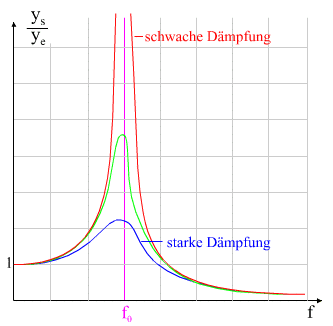
 Ist
das schwingungsfähige System schwach gedämpft, so kann es zur
Resonanzkatastrophe kommen. Die Resonanzstelle ist sehr scharf (rote
Kurve).
Ist das schwingungsfähige System stark gedämpft, so ist die
Amplitude des Schwingers zwar maximal, aber deutlich kleiner als im
schwach gedämpften Fall. Die Resonanzkurve ist breiter und damit der
Resonanzfall experimentell auch leichter aufzufinden (blaue Kurve) Ist
das schwingungsfähige System schwach gedämpft, so kann es zur
Resonanzkatastrophe kommen. Die Resonanzstelle ist sehr scharf (rote
Kurve).
Ist das schwingungsfähige System stark gedämpft, so ist die
Amplitude des Schwingers zwar maximal, aber deutlich kleiner als im
schwach gedämpften Fall. Die Resonanzkurve ist breiter und damit der
Resonanzfall experimentell auch leichter aufzufinden (blaue Kurve) |
|
Eine genauere Beschreibung der
Resonanz mit Simulationen erfolgt auf der untergeordneten Seite
Resonanz.
Eine spezielle Art der
Resonanz stellten zwei gekoppelte Pendel dar. Hier ist der
Energievorrat des Erregers nicht mehr unendlich groß. Weisen beide
Pendel die gleiche Eigenfrequenz auf, so wird im Resonanzfall
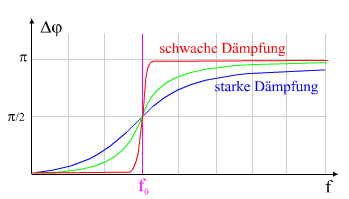
(Phasenverschiebung Δφ = π/2) die
Energie vom Erreger vollständig auf das andere Pendel übertragen
wodurch dieses wiederum zu einem neuen Erreger wird.
Eine genauere Beschreibung der
gekoppelten Pendel mit Simulationen erfolgt auf der untergeordneten Seite
gekoppelte Pendel. |
Wellenarten
|
 Eine
Longitudinalwelle, auch Längswelle genannt, ist eine
physikalische Welle, bei der die Bewegungsrichtung der schwingenden
Teilchen (Luftmoleküle, etc.) in Ausbreitungsrichtung verlaufen. Longitudinalwellen sind
sehr oft Druckwellen (z.B. Schall).
Das bedeutet das sich eine Überdruck (bzw. Unterdruck oder Zug) in
einem Medium in der Ausbreitungsrichtung fortpflanzt
(verschiebt/verbreitet). Die einzelnen Teilchen schwingen hierbei in
der Ausbreitungsrichtung um den Betrag der Amplitude hin und her.
Nach dem Durchlauf der Schwingung bewegen die Teilchen sich wieder
an ihre Ruhestellung zurück. Durch die Ausbreitung der Schwingung
geht keine Energie verloren (abgesehen von Reibungsverlusten
zwischen den Teilchen). Eine
Longitudinalwelle, auch Längswelle genannt, ist eine
physikalische Welle, bei der die Bewegungsrichtung der schwingenden
Teilchen (Luftmoleküle, etc.) in Ausbreitungsrichtung verlaufen. Longitudinalwellen sind
sehr oft Druckwellen (z.B. Schall).
Das bedeutet das sich eine Überdruck (bzw. Unterdruck oder Zug) in
einem Medium in der Ausbreitungsrichtung fortpflanzt
(verschiebt/verbreitet). Die einzelnen Teilchen schwingen hierbei in
der Ausbreitungsrichtung um den Betrag der Amplitude hin und her.
Nach dem Durchlauf der Schwingung bewegen die Teilchen sich wieder
an ihre Ruhestellung zurück. Durch die Ausbreitung der Schwingung
geht keine Energie verloren (abgesehen von Reibungsverlusten
zwischen den Teilchen). |
 Eine
Transversalwelle, oder auch Schubwelle, ist eine
physikalische Welle, bei der die Bewegungsrichtung der schwingenden
Teilchen, bzw. die Feldlinien der beteiligten Felder zur
Ausbreitungsrichtung senkrecht verlaufen. Bei Transversalwellen gibt
es dreidimensional betrachtet zwei Schwingungsebenen, welche
untereinander und zur Ausbreitungsrichtung senkrecht stehen. Eine
Transversalwelle, oder auch Schubwelle, ist eine
physikalische Welle, bei der die Bewegungsrichtung der schwingenden
Teilchen, bzw. die Feldlinien der beteiligten Felder zur
Ausbreitungsrichtung senkrecht verlaufen. Bei Transversalwellen gibt
es dreidimensional betrachtet zwei Schwingungsebenen, welche
untereinander und zur Ausbreitungsrichtung senkrecht stehen. |
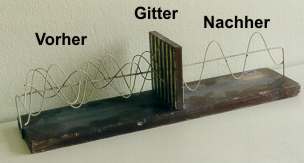 Eine
sehr wichtige Eigenschaft von Transversalwellen ist die Möglichkeit
der Polarisation. Treffen Transversalwellen auf ein Längsgitter, so
kann nur der Schwingungsanteil in Gitterrichtung durch dieses
hindurch. Der andere Teil wird vom Gitter absorbiert. Eine
sehr wichtige Eigenschaft von Transversalwellen ist die Möglichkeit
der Polarisation. Treffen Transversalwellen auf ein Längsgitter, so
kann nur der Schwingungsanteil in Gitterrichtung durch dieses
hindurch. Der andere Teil wird vom Gitter absorbiert. |
|
Die Frequenz f
einer Welle ist deren unveränderliches Merkmal. Hat die Welle in
verschiedenen Medien unterschiedliche
Ausbreitungsgeschwindigkeiten c, so ändert sich die
Wellenlänge l. Es gilt m
c=f l Eine genauere Beschreibung der
Wellenarten mit Simulationen erfolgt auf der untergeordneten Seite
Wellen. |
Wellenwanne
Mechanische und
elektromagnetische Wellen spielen eine große Rolle beim Verständnis
naturwissenschaftlicher Vorgänge. In einer so genannten Wellenwanne wird
Wasser mit Erregern zu Wellenbewegungen angeregt. Die auftretenden
Wellenphänomene können damit gut experimentell untersucht und
verdeutlicht werden. Die bei den Wasserwellen gefundenen
Wellenbeschreibungen können später auch auf die elektromagnetischen
Wellenphänomene übertragen werden. Die Wellenwanne ist damit ein sehr
wichtiges qualitatives Experimentiergerät zum Verständnis der
vielfältigen Wellenphänomene mechanischer und elektromagnetischer
Wellen.
|
|
 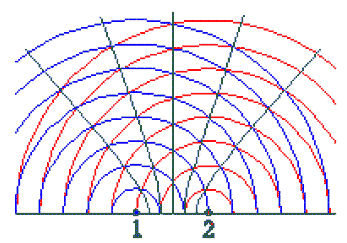 Die Maxima und Minima liegen auf
Kurven, für deren Punkte die Differenz der Abstände (Dr) zu den beiden
Erregerzentren konstant und zwar gleich dem jeweiligen Gangunterschied
ist. Diese Kurven sind Hyperbeln (grün) mit den gemeinsamen
Erregerzentren als Brennpunkt. |
|
Konstruktive Interferenz tritt auf für:
Dj=n 2p
oder
Ds=n l
|
Destruktive Interferenz tritt auf für:
Dj=p
oder
Ds=(n+0,5)l
|
|
Eine genauere Beschreibung der
Wellenwanne mit Simulationen erfolgt auf der untergeordneten Seite
Wellenwanne. |
 Eine anschauliche, konstruktive
Verbindung zwischen Wellen und Strahlen zeigt das Huygens -
Fresnelsche Prinzip. Es besagt, dass man sich jeden Punkt einer
Wellenfront als Ausgangspunkt einer kugelförmigen Elementarwelle denken
kann. Eine anschauliche, konstruktive
Verbindung zwischen Wellen und Strahlen zeigt das Huygens -
Fresnelsche Prinzip. Es besagt, dass man sich jeden Punkt einer
Wellenfront als Ausgangspunkt einer kugelförmigen Elementarwelle denken
kann. |
 Alle diese Kugelwellen überlagern sich dann zu neuen Wellen,
die sich in alle Richtungen ausbreiten. Einige Richtungen sind durch
konstruktive Interferenz besonders bevorzugt: Die Senkrechte zu diesen
Wellenfronten zeigt den dieser Welle entsprechenden „Strahl“. |
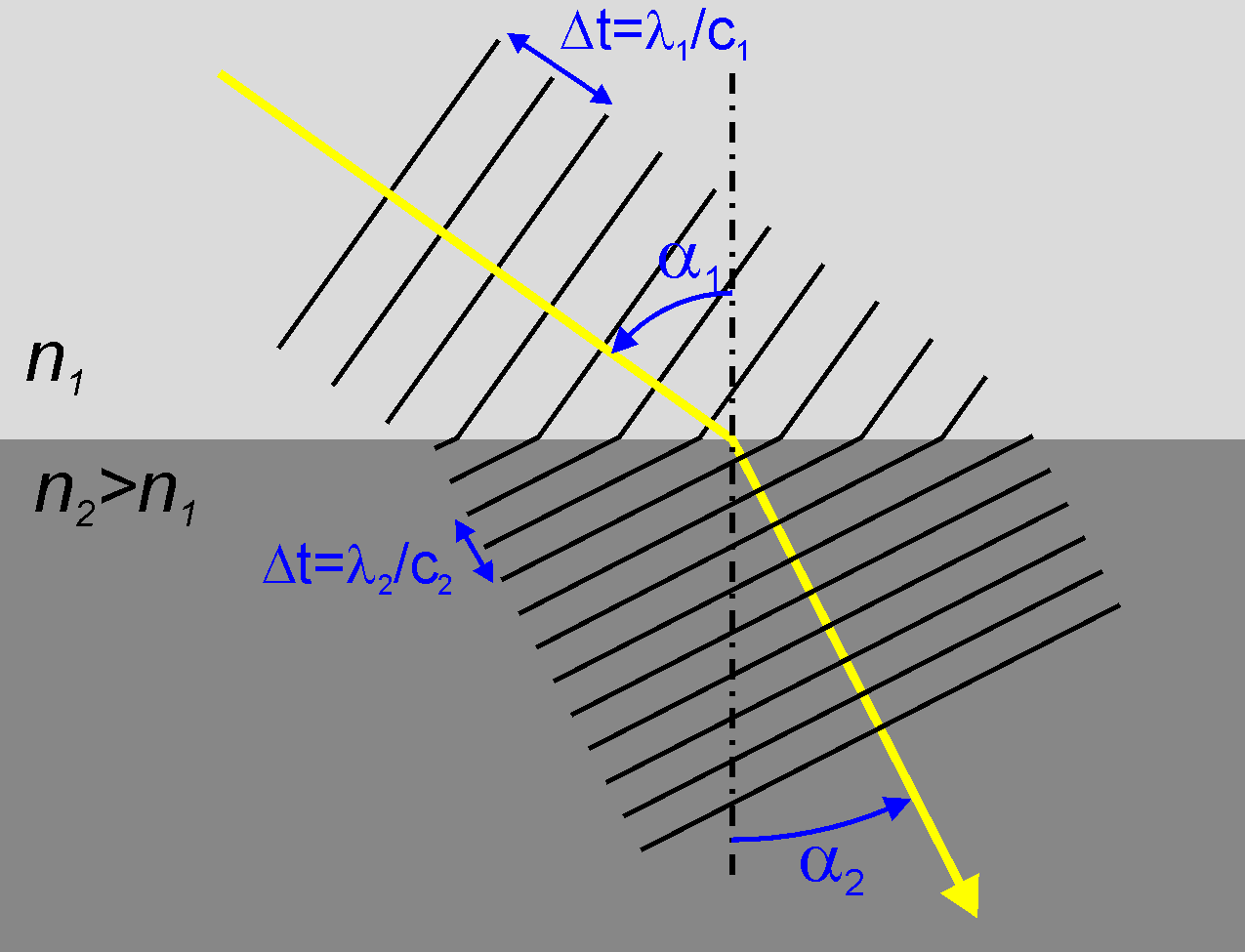 Aus der Optik ist das Phänomen
der Brechung und Reflektion bekannt. Das Gesetz, welches die Reflexion von
Licht an einer Grenzfläche beschreibt ist sehr einfach und gilt an jeder
Grenzfläche zwischen zwei Medien. Es lautet: Einfallswinkel gleich
Reflexionswinkel, wobei die Winkel zum Lot der Grenzfläche gemessen werden.
Dieser Effekt lässt sich auch mit Hilfe der Wellenwanne zeigen.
In tiefem Wasser bewegen sich Wellen schneller als in seichtem.
Die Frequenz als unveränderliches Merkmal einer Welle bleibt
erhalten. Wenn die Ausbreitungsgeschwindigkeit sinkt, so ändert
sich neben einer Verkleinerung der Wellenlänge außerdem die
Richtung der Senkrechten auf der Wellenfront.
Dabei gilt:
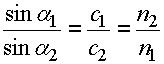
|
letzte Änderung: 23.6.2009 |



















