wobei k die Dämpfung ist. Voraussetzung dafür ist, dass die Dämpfung einen kritischen Wert (kritische Dämpfung) nicht erreicht oder nicht überschreitet. Anderenfalls findet keine Schwingung im eigentlichen Sinne (Oszillation) statt, sondern das System kriecht in die Ruhelage zurück.
























 Als
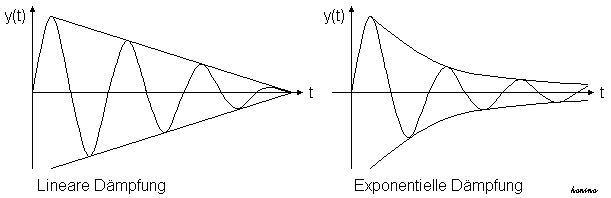
Dämpfung bezeichnet man die Verringerung der Amplitude einer
Schwingung. Die Bilder zeigen einen möglichen zeitlichen Verlauf
einer gedämpften Schwingung.
Als
Dämpfung bezeichnet man die Verringerung der Amplitude einer
Schwingung. Die Bilder zeigen einen möglichen zeitlichen Verlauf
einer gedämpften Schwingung.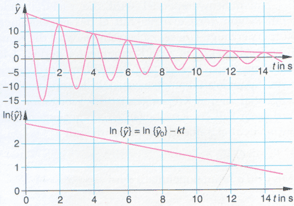 Die
Verringerung der Amplitude ist durch folgende Gesetzmäßigkeit
gekennzeichnet:
Die
Verringerung der Amplitude ist durch folgende Gesetzmäßigkeit
gekennzeichnet: