










untergeordnete
Seiten:
|
Physik, 12 - elektromagnetische
Wellen |
Übersicht
Elektromagnetische Wellen sind die uns im Alltag neben
Wasserwellen und Schallwellen am häufigsten begegnenden
Arten von Wellen. Zu ihnen gehören unter anderem das Licht
(inklusive der Röntgen- und Gammastrahlung) und
Rundfunkwellen. Im Gegensatz zu Schallwellen handelt es
sich, wie bei Wasserwellen, um
Transversalwellen, d.h. Ausbreitungsrichtung und
Schwingungsrichtung stehen senkrecht zueinander, was am
Phänomen der
Polarisation bemerkbar wird.
Hier zwei
Links zum Download aller in dieser Reihe verwendeten Folien
Sammlung elektromagnetische
Wellen (Stand 26.8.05) und
Sammlung Wellenoptik
(Stand 13.9.05)
Wechselstromtechnik
| Elektrizitätswerke liefern die
Energie für die Versorgung der Haushalte. Sie übertragen die Energie
mit Hilfe von Wechselstrom. Die Erzeugung von Wechselstrom wurde schon im
Themengebiet der Magnetfelder / Induktion
besprochen und wird an dieser Stelle vorausgesetzt. Neu hingegen ist das
Verhalten von elektrischen Bauteilen wie Spule und Kondensatoren in einem
Wechselstromkreis. |
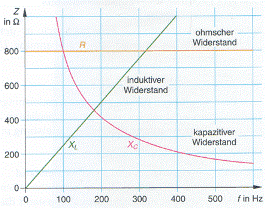
Bei Wechselstrom aber ermöglicht dieser Kondensator infolge
des ständigen Umladens einen Stromfluss, der durch den
Widerstand XC = 1 / ωC
begrenzt wird. C ist dabei die Kapazität des
Kondensators, ω die
Kreisfrequenz der angelegten Spannung. Der Strom baut
die Spannung am Kondensators auf; die Stromstärke
eilt der Spannung um
90° voraus.
Bei einer Spule dagegen folgt die Stromstärke der
Spannung um
90° hinterher; der induktive Widerstand, den die
luftgefüllte Spule dem
Strom entgegensetzt, ist durch XL =ωL
gegeben. |
| Eine genauere Beschreibung der Wechselstromwiderstände erfolgt
auf der untergeordneten Seite
Wechselstrom. |
 Zur
Berechnung weiterer Wechselstromschaltungen ist es zweckmäßig,
Zeigerdiagramme oder komplexe Zahlen zu verwenden. Auf diesem Wege
ergibt sich beispielsweise für den Wechselstromwiderstand (die
Impedanz) einer Reihenschaltung aus ohmschem Widerstand X0,
induktivem Widerstand XL und kapazitivem
Widerstand XC
die Formel: Zur
Berechnung weiterer Wechselstromschaltungen ist es zweckmäßig,
Zeigerdiagramme oder komplexe Zahlen zu verwenden. Auf diesem Wege
ergibt sich beispielsweise für den Wechselstromwiderstand (die
Impedanz) einer Reihenschaltung aus ohmschem Widerstand X0,
induktivem Widerstand XL und kapazitivem
Widerstand XC
die Formel:
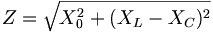
und für den Phasenwinkel φ
errechnet sich
-
tanφ = (XL
− XC) / X0.
|
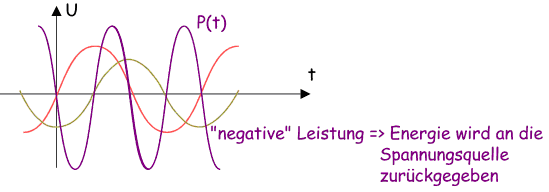 Strom
und Spannung liegen beim Kondensator und der Spule im Gegensatz
zum ohmschen Widerstand nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort. Strom
und Spannung liegen beim Kondensator und der Spule im Gegensatz
zum ohmschen Widerstand nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort. |
|
Im
Wechselstromkreis werden drei Leistungsarten unterschieden.
| 1) |
Die Wirkleistung PW |
| |
Die Wirkleistung
ist die Leistung, welche in einem Wechselstromkreis
tatsächlich abgegeben wird. An einem reinen ohmschen
Widerstand ist PW
= Ueff Ieff
Allgemein gilt:
Stromstärke und Spannung um j
phasenverschoben, so ergibt sich PW
= Ueff Ieff
cos j
Dabei ist
cos j
der so genannte Leistungsfaktor, welcher angibt wie
viel von der Scheinleitung als Wirkleitung zur Verfügung
steht. |
| 2) |
Die Scheinleistung PS |
| |
Die Scheinleitung
ist die Leistung, welche in einem Wechselstromkreis maximal
als Wirkleistung zur Verfügung steht.
PS
= Ueff Ieff |
| 3) |
Die Blindleistung PQ |
| |
Die Blindleistung
ist die Leistung, welche den Wechselstromkreis im
Viertelperiodentakt verlässt und wieder aufgenommen wird.
Sie wird nur zum Aufbau der Felder benötigt und steht dem
Verbraucher nicht zur Verfügung.
PQ
= Ueff Ieff
sin j |
Es gilt: PS²
= PQ² +PS²
|
Schwingkreis
 in
Kreis aus Kondensator und Spule heißt elektrischer Schwingkreis, da
in ihm elektrische Schwingungen stattfinden. Diese sind z.B.
für die Nachrichtentechnik notwendig um elektromagnetische Wellen
abstrahlen zu können. Die Formel für die Periodendauer nennt man zu
Ehren eines bedeutenden britischen Forschers "Thomson-Formel" in
Kreis aus Kondensator und Spule heißt elektrischer Schwingkreis, da
in ihm elektrische Schwingungen stattfinden. Diese sind z.B.
für die Nachrichtentechnik notwendig um elektromagnetische Wellen
abstrahlen zu können. Die Formel für die Periodendauer nennt man zu
Ehren eines bedeutenden britischen Forschers "Thomson-Formel"Eine genauere Beschreibung der
Funktionsweise von elektrischen Schwingkreisen erfolgt
auf der untergeordneten Seite
Schwingkreis. |
Dipol
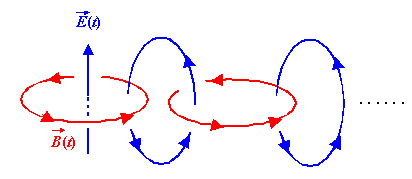 Das
sich zeitlich ändernde elektrische Feld ist - wie der Strom im
Leiter - von kreisförmigen magnetischen Feldlinien umgeben.
Nun ist aber auch das sich zeitlich ändernde
magnetische Feld seinerseits von einem sich zeitlich ändernden
elektrischen Wirbelfeld umschlossen. Dieses wiederum wird von einem
sich zeitlich ändernden Magnetfeld umschlossen, das von einem
elektrischen Wirbelfeld umschlossen wird usw. Das
sich zeitlich ändernde elektrische Feld ist - wie der Strom im
Leiter - von kreisförmigen magnetischen Feldlinien umgeben.
Nun ist aber auch das sich zeitlich ändernde
magnetische Feld seinerseits von einem sich zeitlich ändernden
elektrischen Wirbelfeld umschlossen. Dieses wiederum wird von einem
sich zeitlich ändernden Magnetfeld umschlossen, das von einem
elektrischen Wirbelfeld umschlossen wird usw.
Dies führte Maxwell 1868 zu der Voraussage:
Ein sich zeitlich änderndes
elektromagnetisches Feld breitet sich im Raum als elektromagnetische
Welle aus. |
|
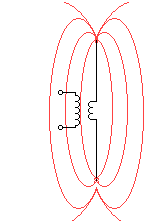 Wenn man in einem Schwingkreis
Kapazität und Induktivität soweit verkleinert, dass die
Kondensatorplatten durch zwei Drahtenden und die Spule durch ein
Leiterstück ersetzt werden kann, dann erhält man, wegen Wenn man in einem Schwingkreis
Kapazität und Induktivität soweit verkleinert, dass die
Kondensatorplatten durch zwei Drahtenden und die Spule durch ein
Leiterstück ersetzt werden kann, dann erhält man, wegen
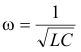 ,
einen Schwingkreis mit hoher Eigenfrequenz. Die für den geraden Draht
eigentlich nicht mehr zutreffende Bezeichnung "Schwingkreis" ersetzt man
nun besser durch "Dipol", zu Ehren von Heinrich Hertz (1857 - 1894)
Hertzscher Dipol genannt. ,
einen Schwingkreis mit hoher Eigenfrequenz. Die für den geraden Draht
eigentlich nicht mehr zutreffende Bezeichnung "Schwingkreis" ersetzt man
nun besser durch "Dipol", zu Ehren von Heinrich Hertz (1857 - 1894)
Hertzscher Dipol genannt.
Im Schwingkreis mit
Plattenkondensator kann das Streufeld am Rande und außerhalb der
Platten meist vernachlässigt werden, weil die Energie im
wesentlichen im homogenen Feld zwischen den Platten lokalisiert ist.
Im Dipol dagegen steckt die ganze Energie in den Streufeldern, weil
es den Bereich des homogenen Feldes zwischen den Platten gar nicht
gibt. |
|
Eine genauere Beschreibung der
Dipolstrahlung erfolgt
auf der untergeordneten Seite Dipol. |
|
Einen ausführlichen Lehrgang zu
elektromagnetischen Wellen findet sich bei:
  |
Beugung am Spalt
|
|
 Das Phänomen selber erinnert allerdings an Versuche mit der
Wellenwanne mit zwei Öffnungen - doch hier ist doch scheinbar nur
eine vorhanden? Das Phänomen selber erinnert allerdings an Versuche mit der
Wellenwanne mit zwei Öffnungen - doch hier ist doch scheinbar nur
eine vorhanden?Zur Erklärung stellt man sich gemäß dem
Huygens´schen Prinzips jeden Punkte
des Spaltes als Ursprung einer Elementarwelle vor.
Bei
geradliniger Ausbreitung bleiben alle Wellen in Phase
(konstruktive Interferenz).
Dies ändert sich jedoch sobald man die
Ausbreitung unter einem Ablenkwinkel betrachtet. Für die beiden
Randstrahlen ergibt sich ein Gangunterschied von
Ds = d sin (a).
Für die Minima gilt
d sin aMin
= ± nl
(n = 1,2,3, ..)
Für die Maxima gilt
d sin aMin
= ±(n+1/2)l
(n = 0,1,2, ..)
Analog
zum Einfachspalt gelten dieselben Bedingungen für
konstruktive oder destruktive Interferenz. Hier ist d jedoch
nicht die Spaltbreite, sondern der Spaltabstand.
Man
muss ebenfalls berücksichtigen, dass sich jeder Spalt zusätzlich noch wie ein
Einfachspalt verhält und mit sich selber interferiert.
Diese beiden
Interferenzen überlagern sich wiederum. |
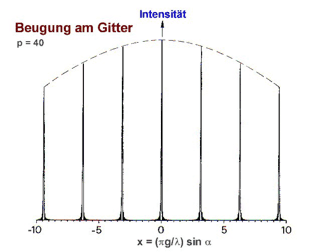  Man kann sagen, dass die Interferenz des Einfachspalts die
Intensitätsverteilung für die Maxima aus der Interferenz des Zweifachsspalts
vorgibt. Bei
genügend großer Spaltanzahl verschwinden die Nebenmaxima praktisch
völlig und es bleiben scharfe Hauptmaxima zurück. Deren Intensität
wird jedoch immer noch von der Interferenz des Einfachsspalts
vorgegeben (gestrichelte Linie). |
Eine genauere Beschreibung der
Beugung am Einfach- und Mehrfachspalt erfolgt
auf der untergeordneten Seite Beugung am
Spalt.
Polarisation
 Eine
sehr wichtige Eigenschaft von Transversalwellen ist die Möglichkeit
der Polarisation. Treffen Transversalwellen auf ein Längsgitter, so
kann nur der Schwingungsanteil in Gitterrichtung durch dieses
hindurch. Der andere Teil wird vom Gitter absorbiert. Eine
sehr wichtige Eigenschaft von Transversalwellen ist die Möglichkeit
der Polarisation. Treffen Transversalwellen auf ein Längsgitter, so
kann nur der Schwingungsanteil in Gitterrichtung durch dieses
hindurch. Der andere Teil wird vom Gitter absorbiert.
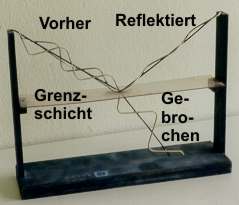
Auch
durch Reflexion an Glas, Wasser oder an einer Wandtafel wird Licht
teilweise polarisiert. Dabei wird der in der Reflexionsebene
polarisierte Anteil des Lichtes zum größeren Teil absorbiert, bzw.
gebrochen.
Für Licht mit einer
Polarisation parallel zur Einfallsebene, welches mit dem
Brewsterwinkel einfällt, entfällt die
Reflexion. Das Licht dringt vollständig durch die Oberfläche.
Licht mit senkrechter Polarisation hingegen wird auch teilweise
reflektiert. Das reflektierte Licht ist somit vollständig linear
polarisiert.
Für die Reflektion an
Licht undurchlässigen Medien gilt: n=tan(aBrewster)
Für die Brechung an Licht
durchlässigen Medien gilt: aBrewster=arctan(n1/n2) |
 Ein
Polarisationsfilter enthält fadenförmige Moleküle welche in einer
bestimmten Richtung ausrichtet sind. Diese wirken diese wie Antennen
auf die Lichtwellen. Alles Licht, dessen elektrische Komponente in
der Richtung der Moleküle schwingt, wird absorbiert. Schwingt die
elektrische Komponente aber senkrecht zum Fadenmolekül, so kann das
Licht durch das Glas hindurch. Ein
Polarisationsfilter enthält fadenförmige Moleküle welche in einer
bestimmten Richtung ausrichtet sind. Diese wirken diese wie Antennen
auf die Lichtwellen. Alles Licht, dessen elektrische Komponente in
der Richtung der Moleküle schwingt, wird absorbiert. Schwingt die
elektrische Komponente aber senkrecht zum Fadenmolekül, so kann das
Licht durch das Glas hindurch. |
 Werden
zwei senkrecht zueinander polarisierte Filter hintereinander
gestellt, so kommt kein Licht durch. Werden
zwei senkrecht zueinander polarisierte Filter hintereinander
gestellt, so kommt kein Licht durch.Dies ist sehr schön im im
Video:  Polarisationsfolien
(499 kB) zu sehen. Polarisationsfolien
(499 kB) zu sehen. |
Eine genauere Beschreibung der
Polarisation und deren Anwendung in der Spannungsoptik oder
Fotografie erfolgt
auf der untergeordneten Seite
Polarisation. Bragg Reflexion
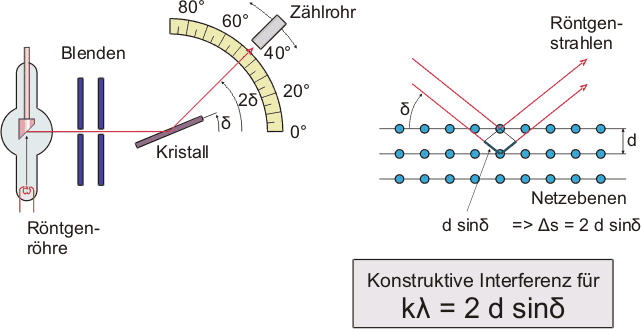 Die
einfallenden Röntgenstrahlenstrahlen werden an den Netzebenen des
Kristalls gebeugt. Dabei gilt Einfallswinkel = Ausfallswinkel.
Verändert man nun den Einfallswinkel, so stellt man Schwankungen in
der Intensität der gebeugten Strahlung fest. Dies liegt an der
Wellennatur der gebeugten Röntgenstrahlung und den
Interferenzerscheinungen zwischen diesen Wellen. Bei bestimmten
Einfallsrichtungen stellt man Maxima fest. Hier addieren sich die
gebeugten Wellen, - sie interferieren konstruktiv
miteinander. Konstruktive Interferenz findet dann statt, wenn der
Gangunterschied der zwischen benachbarten Netzebenen gebeugten
Röntgen-Wellen ein Vielfaches der Wellenlänge beträgt. Die
einfallenden Röntgenstrahlenstrahlen werden an den Netzebenen des
Kristalls gebeugt. Dabei gilt Einfallswinkel = Ausfallswinkel.
Verändert man nun den Einfallswinkel, so stellt man Schwankungen in
der Intensität der gebeugten Strahlung fest. Dies liegt an der
Wellennatur der gebeugten Röntgenstrahlung und den
Interferenzerscheinungen zwischen diesen Wellen. Bei bestimmten
Einfallsrichtungen stellt man Maxima fest. Hier addieren sich die
gebeugten Wellen, - sie interferieren konstruktiv
miteinander. Konstruktive Interferenz findet dann statt, wenn der
Gangunterschied der zwischen benachbarten Netzebenen gebeugten
Röntgen-Wellen ein Vielfaches der Wellenlänge beträgt.
(Beugung an nur zwei Netzebenen würde zu kaum messbarer gebeugter
(reflektierter) Röntgenstrahlung führen. Hierfür ist die Beugung an
einer ganzen Schar von Netzebenen nötig.) |
Der Gangunterschied zwischen den beiden gebeugten Strahlen
entspricht der Strecke Ds=2dsind. Eine genauere Beschreibung der
Bragg Reflexion und deren Anwendung erfolgt
auf der untergeordneten Seite Bragg
Reflexion.
letzte Änderung: 13.9.2005 |



















