parallele Seiten:
            
|
Physik, 12 mechanische
Schwingungen und Wellen - Federpendel und Schwerependel |
Übersicht
Der
wichtigste Schwingungstyp ist die harmonische Schwingung oder die
Sinusschwingung. Das heißt, die Amplitude bleibt konstant - die Schwingung
ist ungedämpft. Er tritt z. B. bei der Projektion einer gleichförmigen
Kreisbewegung oder bei der Schwingung eines Feder- oder Schwerependels auf.
Ein reales Feder- oder
Schwerependel verhält sich in einem nicht zu langen Zeitraum aber mit guter
Nährung wie ein ideales Pendel
Federpendel
Dieses Java-Applet simuliert
ideales (reibungsfrei) Federpendel.
Beobachtet werden können die Elongation,
Geschwindigkeit, Beschleunigung, Kraft und Energie.
|
Die Federkonstante, die Masse des Pendelkörpers, die Fallbeschleunigung
und die Amplitude der Schwingung lassen sich mit Hilfe der
Eingabefelder in gewissen Grenzen variieren. Um diejenige Größe
auszuwählen, deren zeitliche Änderung dargestellt werden soll, muss man
einen der fünf Radiobuttons anklicken.
www.walter-fendt.de/ph11d/federpendel.htm
© Walter Fendt, 24. Mai 1998
|
Aufgaben:
 |
Untersuchen sie wie sich die
einzelnen Größen ändern, wenn man die Federkonstante verdoppelt bzw.
halbiert?
|
|
Untersuchen sie, wie sich die
einzelnen Größen ändern, wenn man die Amplitude verdoppelt bzw.
halbiert?
|
| Untersuchen sie, wie sich die einzelnen Größen ändern, wenn man die
Masse des Pendelkörpers verdoppelt bzw. halbiert? |
Schwerependel
Dieses Java-Applet simuliert
ideales (reibungsfrei) Schwerependel. Bei den Berechnungen wird die geringfügige Abhängigkeit der
Schwingungsdauer von der Amplitude vernachlässigt.
Beobachtet werden können die Elongation,
Geschwindigkeit, Beschleunigung, Kraft und Energie.
|
Die Pendellänge, die Fallbeschleunigung, die Masse des
Pendelkörpers und die Amplitude der Schwingung (in Grad) lassen sich mit
Hilfe der Eingabefelder in gewissen Grenzen variieren. Um diejenige Größe
auszuwählen, deren zeitliche Änderung dargestellt werden soll, muss man
einen der sechs Radiobuttons anklicken.
www.walter-fendt.de/ph11d/ fadenpendel.htm
© Walter Fendt
|
Aufgaben:
|
Untersuchen sie wie sich die
einzelnen Größen ändern, wenn man die Fadenlänge verdoppelt bzw.
halbiert?
|
|
Untersuchen sie, wie sich die
einzelnen Größen ändern, wenn man die Amplitude verdoppelt bzw.
halbiert?
|
|
Untersuchen sie, wie sich die
einzelnen Größen ändern, wenn man die Masse des Pendelkörpers verdoppelt
bzw. halbiert? |
Schwerependel mit großer
Auslenkung
Ein Schwerependel führt
nur für kleine Auslenkungen j eine
harmonische Schwingung aus. Wird die Auslenkung j
zu groß gilt die Näherung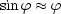 
nicht mehr. Das folgende Java Applet simuliert ein reibungsfreies Pendel
wahlweise bei kleiner oder bei großer Auslenkung.
Die Mathematik besagt, dass die
Näherung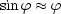
nur für kleine Winkel gilt. Aber wie wirkt sich dann ein großer Winkel beim
Schwerependel aus?
|
|
Wie zu sehen schwingt das Pendel weiterhin regelmäßig. Es führt
jedoch keine harmonische Schwingung aus. Wir erinnern uns:
Ist die rücktreibende Kraft
umso größer je größer die Auslenkung ist (lineares Kraftgesetz F ~
x) so kommt es zu einer harmonischen Schwingung.
Und genau diese Proportionalität gilt für große Auslenkungen
nicht mehr. |
Übrigens: es gibt ein
spezielles Schwerependel bei dem die Schwingungsdauer von der Amplitude
unabhängig ist:
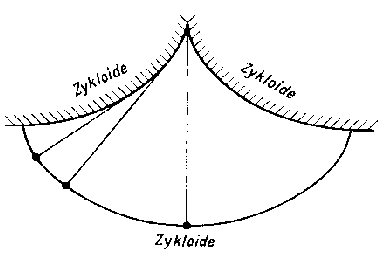
letzte Änderung: 16.3.2005 |
