Home Chemie Physik Sonstiges Schulbilder mich Links

11 Kinematik
11 Dynamik I
11 Dynamik II
11 Gravitation
11+12 Schwingungen
11+12 E-Felder
12 B-Felder
12+13 EM Wellen
13 Quantenphysik
13 Atomphysik
13 Relativität
13 Thermodynamik
Abi-Klausuren

parallele Seiten:

Schwingunsgrößen Schwingung - Kreis math. Beschreibung Pendel Dämpfung Wellenarten Interferenz Doppler Effekt Fourier Resonanz gekoppelte Pendel Wellenwanne Huygens

Physik, 8 Akustik - Dopplereffekt
Java Applet 1 Java Applet 2 Aufgaben

Übersicht

Der Krankenwagen, der einer Person vorbeifährt, der Rennwagen im Fernsehen: sie alle erzeugen den typischen Verlauf von einem hohem zum tiefen Ton. Wer sich nicht erinnern kann: hier eine Hörprobe: carhorn.wav 

Diesen nach seinem Entdecker (Christian Doppler) benannten Dopplereffekt hört man, wenn sich eine Schallquelle und Zuhörer zueinander bewegen. Nähern sich Schallquelle und Zuhörer einander an, so hört man einen höheren Ton. Bewegt sie sich voneinander weg, so hört man einen tieferen Ton.
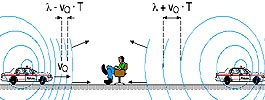Bei einem ruhendem Sender beträgt der Abstand zwischen den Wellenfronten immer genau eine Wellenlänge l. Bewegt sich der Sender jedoch mit v0 auf Beobachter zu, so verkürzt sich dieser Abstand, da der Sender sich zur gleichen Zeit (Periodendauer T) um v0T fortbewegt hat. Es gilt:

lBeobachter=lSender-v0T

Fährt er weg so gilt: lBeobachter=lSender+v0T

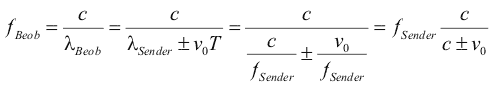
Bewegt sich der Wellenerreger mit der Ausbreitungsgeschwindigkeit (v0=c), so geht f gegen unendlich. Außerdem addieren sich direkt vor der Quelle die Amplituden vieler Wellen auf. Dies ist umgangssprachlich die Schallmauer.

Java Applet 1: Der Dopplereffekt

Ein Notarztwagen fährt mit eingeschaltetem Martinshorn an einer Person vorbei, die an der Straße steht. Der Notarztwagen ist somit ein bewegter Sender. Dieser gibt im entsprechend seiner Tonlage Schallwellen ab. Achte darauf, ob die Wellenfronten im selben Rhythmus bei Zuhörer (Person) ankommen.

Wie ist die Situation, nachdem der Wagen an der Person vorbeigefahren ist? Ändert sich der Rhythmus?

Bemerkung: In einer Hinsicht ist dieses Applet ausgesprochen unrealistisch: Damit der Doppler-Effekt deutlich zu erkennen ist, laufen die Schallwellen hier viel langsamer als in Wirklichkeit.

Die Copyrights für dieses Applet liegen bei URL: http://home.a-city.de/walter.fendt/phd/doppler.htm
© Walter Fendt, 25. Februar 1998

zurück zum Seitenanfang

Java Applet 2:

Hier habt ihr die Möglichkeit die Geschwindigkeit der sich bewegenden Schallquelle selber einzugeben.

Für unsere Zwecke reicht die klassische (classic) Sichtweise. Das Applet kann auch die Zeitdehnung (relativistic) mit einberechnen, dies führt für unsere Zwecke allerdings zu weit.

Der Zahlenwert 1.0 meint hierbei, dass sich der Sender exakt mit Schallgeschwindigkeit bewegt. Werte kleiner als 1 sind also langsamer und Werte größer 1 dementsprechend schneller als die Schallgeschwindigkeit.

Die Copyright für dieses Applet liegen bei:

zurück zum Seitenanfang

Aufgaben

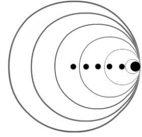
Das Bild zeigt die Kreiswellen, welche beim "Steine-Flitschen" auf einer Wasseroberfläche entstehen. Wie ist hier das Verhältnis von Erregerfrequenz und Ausbreitungsgeschwindigkeit?

zurück zum Seitenanfang

 

letzte Änderung: 9.5.2005