










parallele Seiten:
|
Physik, 12 EM Felder und Wellen - Wechselstromkreise |
Übersicht
Unter Wechselstrom
versteht man elektrischen Strom, dessen Betrag und Richtung (Polung)
sich nach einer konstanten Periodendauer wiederholt. Dies wird im
Englischen auch als "Alternating Current" (AC) bezeichnet. Dabei
verschwindet der Mittelwert, d. h. während einer Periode wird die
gleiche Ladungsmenge in beiden Richtungen transportiert. Das ist z. B.
bei dem technisch wichtigen sinusförmigen "Steckdosenstrom" der Fall.
Wechselstromwiderstände
Dieses Java-Applet zeigt einen
einfachen Stromkreis, der aus einer Wechselspannungsquelle und - je nachdem,
welcher der drei Radiobuttons aktiviert ist - einem reinen Ohmschen Widerstand,
einem Kondensator oder einer idealen Induktionsspule (ohne Ohmschen Widerstand)
besteht. Zusätzlich sind Messgeräte für Spannung U (blau) und Stromstärke I
(rot) vorhanden.
|
Unterhalb der Schaltskizze sieht man links ein Zeigerdiagramm:
Aus der Position der beiden Zeiger (blau für die Spannung, rot für
die Stromstärke) kann man jeweils die Schwingungsphase ablesen. Die
Projektion eines Zeigers auf die senkrechte Achse ergibt den
momentanen Wert von U bzw. I. Rechts unten wird in einem t-U- bzw.
t-I-Diagramm die Zeitabhängigkeit von Spannung und Stromstärke
dargestellt. Der "Reset"-Button bringt den Stromkreis in den
Anfangszustand. Mit dem anderen Schaltknopf kann man die Simulation
starten, unterbrechen und wieder fortsetzen. Die Option "Zeitlupe"
bewirkt eine Verlangsamung um den Faktor 5. |
© Walter Fendt, 13. Juni 1998
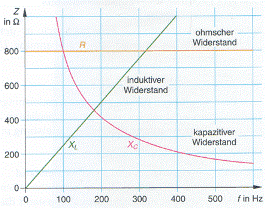 Kondensatoren und Spulen verhalten sich wegen der
dauernden Stromänderung bei Wechselstrom anders als bei
Gleichstrom. Dort lässt ein Kondensator nur für die
Dauer des Aufladens ein Stromfließen zu, danach bildet
der Kondensator eine Unterbrechung des Stromkreises. Kondensatoren und Spulen verhalten sich wegen der
dauernden Stromänderung bei Wechselstrom anders als bei
Gleichstrom. Dort lässt ein Kondensator nur für die
Dauer des Aufladens ein Stromfließen zu, danach bildet
der Kondensator eine Unterbrechung des Stromkreises.Bei Wechselstrom aber ermöglicht dieser Kondensator infolge
des ständigen Umladens einen Stromfluss, der durch den
Widerstand XC = 1 / ωC
begrenzt wird. C ist dabei die Kapazität des
Kondensators, ω die
Kreisfrequenz der angelegten Spannung. Der Strom baut
die Spannung am Kondensators auf; die Stromstärke
eilt der Spannung um
90° voraus.
Bei einer Spule dagegen folgt die Stromstärke der
Spannung um
90° hinterher; der induktive Widerstand, den die
luftgefüllte Spule dem
Strom entgegensetzt, ist durch XL =ωL
gegeben. |
Zur Berechnung weiterer Wechselstromschaltungen ist es
zweckmäßig,
Zeigerdiagramme oder komplexe Zahlen zu verwenden. Auf
diesem Wege ergibt sich beispielsweise für den
Wechselstromwiderstand (die Impedanz) einer
Reihenschaltung aus ohmschem Widerstand X0,
induktivem Widerstand XL und kapazitivem
Widerstand XC die Formel:
-
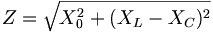
und für den Phasenwinkel φ
errechnet sich
-
tanφ = (XL
− XC) / X0.
Zeigerdiagramme
Wie schon bei der
Projektion von Kreisbewegungen als
mechanischen Schwingungen werden auch die Wechselstromgrößen als eine
harmonische Schwingung mit der Kreisfrequenz ω aufgefasst, dem so
genannten Zeigerdiagramm. Die Spannung / der Strom wird hier durch einen
rotierenden Zeiger, der mit dieser Winkelgeschwindigkeit umläuft, und dessen
Länge die Amplitude der Schwingung ist dargestellt. Die tatsächliche
physikalische Messgröße ist dann die Projektion des Zeigers auf Y-Achse.
Das Zeigerdiagramm ermöglicht eine
einfache Beschreibung von Phasenverschiebungen zwischen Schwingungen. Wenn
Schwingungen mit der gleichen Frequenz f erfolgen, können sie sich
noch in der Amplitude (= Länge des Zeigers) und im Phasenwinkel
unterscheiden.

Letzterer gibt an, um welchen Winkel sie gegenüber einer Sinuskurve
verschoben sind. Zwei Schwingungen, die sich im Phasenwinkel um Δφ
unterscheiden, stellt man im Zeigerdiagramm durch zwei Zeiger dar,
die um eben diesen Winkel gegeneinander verdreht sind.
Die blaue Schwingung läuft der violetten um 90°
= π/2 in der Phase nach |
 Die
blaue Schwingung läuft der violetten um 90° = π/2 in der Phase
voraus Die
blaue Schwingung läuft der violetten um 90° = π/2 in der Phase
voraus |
| Phasenverschiebungen treten zum Beispiel in der
Wechselstromlehre zwischen Strom und Spannung auf, wenn Spulen oder
Kondensatoren in einer Schaltung enthalten sind. Strom und Spannung
werden dann im Zeigerdiagramm dargestellt, wo sich auch bei
komplizierten Schaltungen Gesamtstrom oder Gesamtspannung durch
Addition der Zeiger bestimmen lassen. Hieraus ergibt sich dann
geometrisch sowohl die Amplitude als auch die Phasenlage der
resultierenden Schwingung. Das
ohmsche Gesetz
(R=U/I) kann auf komplexe Zahlen angewendet werden und führt dann zu
einer Beschreibung von Spulen und Kondensatoren durch komplexe
Widerstände. |
Effektivwerte und Leistung im Wechselstromkreis
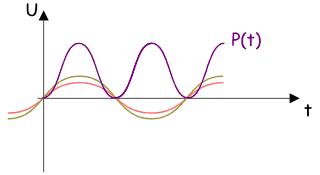 Bei
einem ohmschen Widersand liegen Spannung und Strom in Phase. Die
Leistung als Produkt von Spannung und Stromstärke P=UI
ist dadurch immer positiv. Die Energie wird im Widerstand in
Wärme umgewandelt und verlässt dadurch den Wechselstromkreis. Bei
einem ohmschen Widersand liegen Spannung und Strom in Phase. Die
Leistung als Produkt von Spannung und Stromstärke P=UI
ist dadurch immer positiv. Die Energie wird im Widerstand in
Wärme umgewandelt und verlässt dadurch den Wechselstromkreis.
Die Arbeit ergibt sich zu W= R I² T |
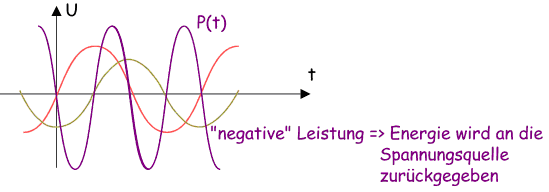 Strom
und Spannung liegen nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort. Strom
und Spannung liegen nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort.Die Arbeit ergibt sich zu
W = R I²max T /2 |
Vergleicht man die an einem ohmschen Widerstand geleistete
Arbeit mit der Arbeit an einer Spule, so unterscheiden sie sich
um den Faktor 1/2. Der Effektivwert einer Wechselspannung ist
nun genau die Stromstärke bei der ein Gleichstrom dieselbe
Arbeit leisten würde. Da die Stromstärke quadratisch in die
Berechnung der Arbeit eingeht, so ergibt sich die
Effektivstromstärke Ieff, zu
 und analog die Effektivspannung
zu und analog die Effektivspannung
zu
 . .
Bei nicht-sinusförmigen Strömen ergeben sich andere
Effektivwerte, diese werden im Rahmen des Unterrichts aber
nicht behandelt.
Falls nichts anderes gesagt
wird, sind bei Wechselströmen / Wechselspannungen immer die
Effektivwerte gemeint. |
|
Im
Wechselstromkreis werden drei Leistungsarten unterschieden.
| 1) |
Die Wirkleistung PW |
| |
Die
Wirkleistung ist die Leistung, welche in einem
Wechselstromkreis tatsächlich abgegeben wird. An einem
reinen ohmschen Widerstand ist PW
= Ueff Ieff
Allgemein
gilt: Stromstärke und Spannung um
j phasenverschoben, so ergibt
sich PW =
Ueff Ieff
cos j
Dabei ist
cos
j der so genannte
Leistungsfaktor, welcher angibt wie viel von der
Scheinleitung als Wirkleitung zur Verfügung steht. |
| 2) |
Die Scheinleistung PS |
| |
Die
Scheinleitung ist die Leistung, welche in einem
Wechselstromkreis maximal als Wirkleistung zur Verfügung
steht.
PS
= Ueff Ieff |
| 3) |
Die Blindleistung PQ |
| |
Die
Blindleistung ist die Leistung, welche den
Wechselstromkreis im Viertelperiodentakt verlässt und
wieder aufgenommen wird. Sie wird nur zum Aufbau der
Felder benötigt und steht dem Verbraucher nicht zur
Verfügung.
PQ
= Ueff Ieff
sin j |
Es gilt: PS²
= PQ² +PS²
|
letzte Änderung: 20.7.2005 |


























 Kondensatoren und Spulen verhalten sich wegen der
dauernden Stromänderung bei Wechselstrom anders als bei
Gleichstrom. Dort lässt ein Kondensator nur für die
Dauer des Aufladens ein Stromfließen zu, danach bildet
der Kondensator eine Unterbrechung des Stromkreises.
Kondensatoren und Spulen verhalten sich wegen der
dauernden Stromänderung bei Wechselstrom anders als bei
Gleichstrom. Dort lässt ein Kondensator nur für die
Dauer des Aufladens ein Stromfließen zu, danach bildet
der Kondensator eine Unterbrechung des Stromkreises.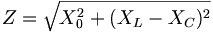
 Bei
einem ohmschen Widersand liegen Spannung und Strom in Phase. Die
Leistung als Produkt von Spannung und Stromstärke P=UI
ist dadurch immer positiv. Die Energie wird im Widerstand in
Wärme umgewandelt und verlässt dadurch den Wechselstromkreis.
Bei
einem ohmschen Widersand liegen Spannung und Strom in Phase. Die
Leistung als Produkt von Spannung und Stromstärke P=UI
ist dadurch immer positiv. Die Energie wird im Widerstand in
Wärme umgewandelt und verlässt dadurch den Wechselstromkreis. Strom
und Spannung liegen nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort.
Strom
und Spannung liegen nicht in Phase. Die Leistung ist daher mal
positiv (Energie wird in den Kondensator / die Spule
transportiert) und mal negativ (Energie fließt vom Kondensator /
Spule wieder zurück). Dies hat zur Folge, dass an idealen
Bauteilen (kein Widerstand) keine Energie das System verlässt,
sie ändert nur periodisch ihren Ort. und analog die Effektivspannung
zu
und analog die Effektivspannung
zu
 .
.