parallele Seiten:
     
|
Physik, 12 EM Felder und Wellen - elektrischer
Schwingkreis |
Übersicht
 Ein Kreis aus Kondensator und
Spule heißt elektrischer Schwingkreis, da in ihm elektrische
Schwingungen stattfinden. Diese sind z.B. für die
Nachrichtentechnik notwendig um elektromagnetische Wellen abstrahlen zu
können. Die Formel für die Periodendauer nennt man zu Ehren eines
bedeutenden britischen Forschers "Thomson-Formel". |
elektrischer Schwingkreis
|
Nach Betätigung des "Reset"-Buttons werden die
Platten des Kondensators aufgeladen, und zwar die obere Platte
positiv, die untere negativ. Sobald man mit der Maus auf "Start"
klickt, wird durch Umlegen des Schalters die Schwingung in Gang
gesetzt. Mit Hilfe der vier Textfelder lassen sich die Werte für die
Kapazität des Kondensators (100 mF bis 1000 mF), die Induktivität
(1 H bis 10 H) und den Widerstand (0 bis 1000 Ohm) der Spule sowie
für die Batteriespannung variieren. Im Schaltbild sind das
elektrische Feld des Kondensators (rot) und das magnetische Feld der
Spule (blau) durch Feldlinien angedeutet. Dabei ist die Dichte der
Feldlinien ein Maß für die Stärke des jeweiligen Feldes. Zusätzlich
sind die Ladungsvorzeichen der beiden Kondensatorplatten und Pfeile
für die (technische) Stromrichtung zu sehen. © Walter Fendt, 23. Oktober 1999 |
Die Physlet Simulation geht über
die Simulation von Fendt hinaus. Hier kann das System auch bei
angeschlossener Spannungsquelle (also beim Laden des Kondensators)
betrachtet werden (dafür auf Schalter an/aus klicken).
UC
Kondensator
- UR
Widerstand (prop. Strom)
Analogie Federpendel
Schwingkreis
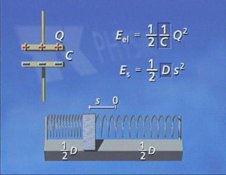 Man
kann zwischen der Schwingung eines Federpendels aus dem Bereich der
Mechanik einem elektrischen Schwingkreis eine Analogiebetrachtung
aufstellen. Dazu wird als erstes ein Bauteil benötigt, das
"potenzielle Energie" elektrische Energie speichern und abgeben
kann. Hierzu eignet sich ein Kondensator. Für seine Energie wird
eine Formel abgeleitet, die sich ganz analog zur potenziellen
Energie einer Feder formulieren lässt: Die Ladung Q des
Kondensators entspricht der Auslenkung s der Feder, der Kehrwert der
Kapazität 1/C der Federhärte D. |
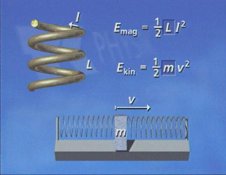 Das
zweite elektrische Bauteil muss der Bewegungsenergie des Gleiters
entsprechen; dafür eignet sich eine Spule. Auch hierfür werden
Formeln angegeben: Die Stromstärke I in der Spule entspricht
der Geschwindigkeit v des Gleiters, die Induktivität L
der Spule der Masse m des Gleiters. Insgesamt erhält man vier
Formeln für verschiedene Energieformen, je zwei, die man als
potenzielle Energien erkennen kann und zwei, die man im weiteren
Sinne als "kinetische" Energien betrachten kann. |
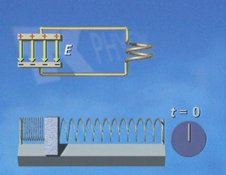 Beide
Schwingungen werden so gestartet, dass die potenzielle Energie
maximal ist. Bei der Feder ist die Dehnung maximal, beim Kondensator
das elektrische Feld. Beim Federpendel setzt sich nun eine Masse
gegen den Widerstand ihrer Trägheit in Bewegung und nimmt
Geschwindigkeit auf, beim Schwingkreis wächst ein Stromfluss gegen
den Widerstand der Induktivität der Spule. |
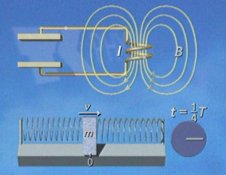 Nach
einer 1/4 Periode t = 1/4 T sind beide potenzielle
Energien null; im Gegenzug sind die Geschwindigkeit der Masse und
die Stromstärke in der Spule maximal. Beide Schwingungen haben
gerade ihren "Nulldurchgang". Bei der Spule ist das magnetische Feld
maximal, während das elektrische Feld des Kondensators gerade
verschwunden ist. |
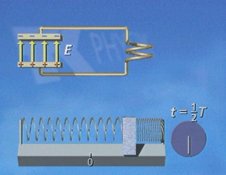 Nach
der halben Schwingungsdauer t = 1/2 T ist wieder die
Ausgangssituation gegeben, aber jeweils versehen mit einem
umgekehrten Vorzeichen: Bei der Feder ist die Auslenkung, beim
Kondensator ist die Feldstärke umgekehrt gerichtet wie zu Beginn.
Bei beiden Schwingungen wechselt die Energie periodisch von
potenzieller zu "kinetischer" Energie und zurück; einmal ist die
"Auslenkung" maximal, dann wieder die Änderung der "Bewegung". |
Zeigerdiagramme im Schwingkreis
Es ist nicht besonders schwierig, aus den Kenngrößen L, R und C eines
Serienschaltkreises und der Frequenz ω
den Wechselstromwiderstand X und die
Spannungsverhältnisse im Stromkreis zu bestimmen (siehe
Wechselstrom). Schwieriger ist es schon,
Fragen nach den Auswirkungen zu beantworten, die eine Änderung der
Schaltkreisparameter hat:
|
Die Summe aller Spannungen in einem Stromkreis ist zu jedem Zeitpunkt
null (Kirchhoff´sche Maschenregel). UL
+ UR + UC
= UQuelle
Für die Resonanzfrequenz
des Schwingkreises gilt die Thomson´sche Schwingungsformel:
 |
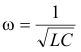Arbeitsaufträge:
- Berechne für eine beliebe Kombination aus Induktivität und
Kapazität die Resonanzfrequenz.
- Stelle die Wechselspannung im Applet auf die
Resonanzfrequenz ein. Was passiert mit der Phasenlage der
Spannung vom Widerstand in diesem Fall? Tipp: dies ist im
Zeigerdiagramm besonders gut zu sehen.
- Verkleinere / vergrößere den ohmschen Widerstand. Was
passiert mit den Spannungsabfällen an den einzelnen Bauteilen
und an welches Phänomen aus den mechanischen Wellen erinnert
dies?
Die den Berechnungen zugrunde liegenden
Formeln lauten für die Impedanz X(ω) und die
Phasenverschiebung f (ω) zwischen Strom und Spannung:
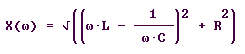und
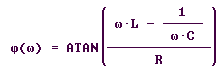
Die
Spannungsabfälle an
Widerstand R, Spule L und Kondensator C ergeben sich aus
den Formeln:
|
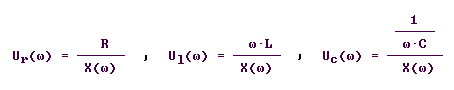
letzte Änderung:
8.4.2005 |
