Übersicht
Hier finden sich zur Zeit nur
Bruchstücke, welche ich selber im Netz aufgetrieben habe. Wird erweitert
und geordnet, sobald ich wieder eine neunte Klasse habe.
Linsenabbildung
Im folgenden Appletfenster können
die roten Punkte und F1 durch Ziehen mit der Maus bewegt werden. Auf diese
Weise lassen sich f, g und G einstellen. Durch Anklicken der Schaltflächen
werden zusätzliche Elemente ein- oder ausgeblendet. Der Schalter zum
Einschalten des virtuellen Bildes sollte nur betätigt werden, wenn der
Gegenstand PQ zwischen F1 und der Linse steht.
Reset durch Eintippen von "r"
Aufgaben
- Führe zunächst ein Realexperiment mit einer Linse der Brennweite
10 cm durch, bei dem für verschiedene Gegenstandsweiten g die zugehörigen
Bildweiten b bestimmt werden (ca. 5 - 6 Werte).
- Betrachte im Appletfenster oben den Strahlengang für die drei
Hauptstrahlen (gelb) und erläutere wie die Strahlen gezeichnet
werden.
- Schalte jetzt das Lichtbündel ein und stelle durch Ziehen an F1 für
f den gleichen Wert wie im Realexperiment ein. Stelle nacheinander die
gleichen Werte für g ein wie im Realexperiment und bestimme die zugehörigen
b. Vergleiche die Ergebnisse der Simulation mit denen aus dem
Experiment. Was lässt sich feststellen. Ist das geometrische Modell
geeignet für die Darstellung der realen Verhältnisse?
- Addiere jeweils mit einem Taschenrechner die Kehrwerte von g und b.
Was stellt man fest? Formuliere die Erkenntnisse als ein Gesetz für
Abbildungen an Linsen. Warum dieses gilt, erfahren wir, wenn wir Fortsetzung
anklicken.
- Ziehe nun den Punkt Q so nahe an die Linse heran, dass b < f ist.
Offenbar treffen sich jetzt die Strahlen nach der Brechung an der
Linse nicht mehr. Klicke jetzt mit der linken Maustaste auf die
Schaltfläche "Virtuelles Bild an" und interpretiere die
dargestellte Zeichnung. Inwiefern gilt das Linsengesetz aus Aufgabe 4
unter diesen Umständen?
© F.
W. Dustmann

Herleitung der Linsengleichung
Reset durch Eintippen von "r"
Aufgaben
- Schalte die 1. Figur ein und bewege den Punkt P auf und ab.
Beobachte dabei die Flächenmessung links unten. Was lässt sich über
die Größe der roten und blauen Fläche aussagen?
- Versuche das Ergebnis von Aufgabe 1 zu begründen. Wenn du dafür
Hilfe brauchst, klicke auf Hilfe.
- Schreibe das Ergebnis von Aufgabe 1 auch als Formel mit den
Variablen G, B, g und b.
- Schalte nun die 1. Figur aus und die 2. an und führe die gleichen
Überlegungen wie in Aufgabe 1 und 3 durch. Jetzt wird in der Formel
allerdings f statt b benötigt.
- Offenbar ist der Abstand des Bildes von der Linse nicht von der Größe
des Gegenstandes, sondern nur von dessen Abstand g von der Linse abhängig.
Deshalb versuchen wir aus den beiden Gleichungen von Aufgabe 3 und 4
die Größen G und B zu beseitigen, so dass wir nur noch eine
Gleichung mit den Variablen g, b und f bekommen. Wie lautet diese
Gleichung.
- Zeige, dass man diese Gleichung auch in der einprägsamen Form
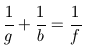 schreiben
kann.
schreiben
kann.
Hilfe 1: Flächenvergleich
Durch Ziehen am Punkt E kann man die farbigen Flächen verändern.
Stelle fest, für welche Lagen von E die rote und die blaue Fläche gleich
sind. Begründe, warum dies so ist. Welche Rolle spielen dabei die
Dreiecke?
Bei diesem Applet können die Brechungsindizes der Medien, sowie der
Einfallswinkel des Lichtstrahls verändert werden. Der Brechungswinkel
und der Totalreflektionswinkel werden berechnet und angezeigt.
a) Überprüfen Sie Ihre Teilergebnisse aus Aufgabe 1 mit Hilfe des
Applets.
b) Berechnen Sie die Grenzwinkel der Totalreflexion für die
Kombinationen von Brechungsindizes (n1=1,1 und n2=1), (n1=1,4 und
n2=1,1), (n1=2 und n2=1,1) und überprüfen Sie Ihre Ergebnisse mit Hilfe
des Applets.
c) Überprüfen Sie bei welcher Kombination von n1 und n2 der
Strahl zum Lot hin gebrochen und bei welcher er vom Lot weg gebrochen
wird.
Prismas.