










parallele Seiten:
|
Physik, 12 mechanische
Schwingungen und Wellen - Resonanz |
Übersicht
Resonanz: ist das Anwachsen der Amplitude (Schwingungsweite,
Auslenkung) einer mechanischen oder elektrischen Schwingung,
dadurch, dass eine äußere Kraft das schwingende System
periodisch "im richtigen Takt" anregt.
Das funktioniert also nur, wenn sie dies genau mit der
"richtigen" Frequenz, d.h. der Eigenfrequenz des
Systems (oder einem Vielfachen davon) macht. |
|
| Eigenfrequenz: ist die Frequenz, mit der ein System frei schwingt. Jedes
System hat dabei ganz bestimmte Eigenfrequenzen. Sie hängen
von den physikalischen Gegebenheiten des Systems (z.B.
Masse, Pendellänge, Federhärte, usw. ab). Anders gesagt,
alle schwingungsfähigen Systeme haben eine Eigenfrequenz,
und wenn wir es mit dieser Eigenfrequenz zum Schwingen
bringen, kann sich die Schwingung zu riesigen Werten
"aufschaukeln". |
|
Resonanz beim Schaukeln
 Klingt
kompliziert .........? Klingt
kompliziert .........?
Ist es aber nicht, jeder kennt das von der
Kinderschaukel her!
Wenn du eine Person auf einer
Schaukel anstoßen möchtest, dann muss man die Person
immer zum richtigen Zeitpunkt anstoßen, d.h. während
jeder Schaukelbewegung genau einmal und im
Umkehrpunkt.
Vielleicht muss man dazwischen auch
mal "aussetzen". Sonst kann es passieren, dass sich
die Schwingungsbewegung zu sehr zur Resonanz
"aufschaukelt" (wie bei dem
Äffchen). |
 Denn
wenn man zu langsam anregst, dann verpasst man die Schaukel
an der richtigen Stelle. Dasselbe passiert, wenn man
zu schnell anregen will, auch in diesem Fall ist die
Schaukel noch nicht wieder am richtigen Punkt und
der Anstoß geht ins Leere. Denn
wenn man zu langsam anregst, dann verpasst man die Schaukel
an der richtigen Stelle. Dasselbe passiert, wenn man
zu schnell anregen will, auch in diesem Fall ist die
Schaukel noch nicht wieder am richtigen Punkt und
der Anstoß geht ins Leere.In
der Animation regt das Äffchen zu schnell an.
Manchmal scheint sich eine Resonanz aufzubauen, dann
ebbt sie wieder ab.
Das Äffchen rettet zwar sein Gesicht, aber es kommt
nicht zur Resonanz! |
|
|
Java Simulation
|
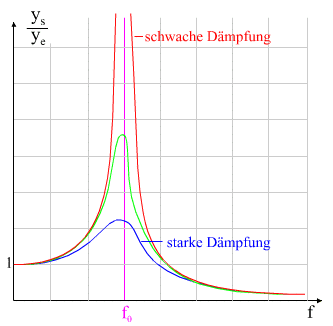 Ist
das schwingungsfähige System schwach gedämpft, so kann es zur
Resonanzkatastrophe kommen. Die Resonanzstelle ist sehr scharf (rote
Kurve). Ist
das schwingungsfähige System schwach gedämpft, so kann es zur
Resonanzkatastrophe kommen. Die Resonanzstelle ist sehr scharf (rote
Kurve).
Ist das schwingungsfähige System stark gedämpft, so ist die
Amplitude des Schwingers zwar maximal, aber deutlich kleiner als im
schwach gedämpften Fall. Die Resonanzkurve ist breiter und damit der
Resonanzfall experimentell auch leichter aufzufinden (blaue Kurve)
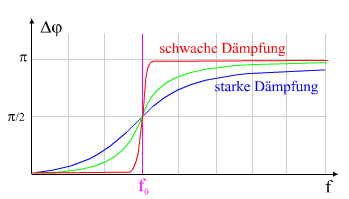 Wird ein schwingungsfähiges System mit der Eigenfrequenz f0
(z.B. Federpendel) durch einen Erreger zu Schwingungen angeregt, so
kann man abhängig von der Erregerfrequenz f folgende Extremfälle
unterscheiden: |
|
|
 | f << f0 (niederfrequenter
Bereich)
Erreger und Schwinger haben keinen Phasenunterschied. Die beiden
Schwingungen haben etwa die gleiche Amplitude, d.h. das
Amplitudenverhältnis ist ungefähr 1. |
 | f = f0
(Resonanzfall)
Der Erreger eilt dem Schwinger um die Phase Δφ = π/2 voraus. Die
Amplitude des Schwingers ist maximal. |
 | f >> f0 (hochfrequenter
Bereich)
Erreger und Schwinger besitzen die Phasenverschiebung Δφ = π.
Die Amplitude des Schwingers geht gegen Null. |
|
|
|
|
Beispiele
Beispiel: Zerbrechen oder "Zersingen" eines
Glases.
Wenn ein
Sänger (oder eine Sängerin) genau die Eigenfrequenz
eines Weinglases trifft, dann kann er /sie mehr
Energie in das Weinglas stecken, als dieses
verkraften kann. Das Glas wird in immer stärkere
Schwingungen versetzt und platzt schließlich. Der
Trick besteht darin, den richtigen Ton zu treffen
und zu halten. Es genügt also nicht, laut und
schrecklich zu grölen! Es wird auch nicht gelingen
das ganze Glas zu zerstören, weil jeder Teil des
Glases eine andere Eigenfrequenz hat! (Das Glas ist
verschieden dick).
 Video:
Glass (98 kB) Video:
Glass (98 kB) |
Beispiel: Resonanz wird verwendet, um einen
Nierenstein zu zertrümmern.
Viele Leute leiden an
Nierensteinen. Bestimmte Mineralien
werden dabei in der Niere nicht
zersetzt und lagern sich zusammen,
ein Nierenstein bildet sich. Wenn er
die Harnröhre verstopft, kann die
Harnflüssigkeit nicht mehr
abfließen. Dies kann
lebensgefährlich sein.
Der Nierenstein müsste
herausoperiert werden. Als
Alternative kann man aber oft
Ultraschallwellen auf den
Nierenstein einwirken lassen. Trifft
man die richtige Frequenz platzt der
Nierenstein in kleine Bruchstücke,
die den Harnleiter passieren und den
Körper so verlassen können. Eine
Operation kann so vermieden werden.
 Video:
Nierenstein Film (82 kB) Video:
Nierenstein Film (82 kB) |
  Beispiel:
Resonanzkatastrophe bei der
Takomabrücke 1940, Spannweite 843m Beispiel:
Resonanzkatastrophe bei der
Takomabrücke 1940, Spannweite 843m
Bereits kurz nach Eröffnung der
Brücke zeigte sich, dass die
Konstruktion sehr empfindlich auf
Seitenwind reagierte. Dies ist
zunächst nichts ungewöhnliches für
Hängebrücken, die systembedingt
immer unter dieser Schwäche leiden.
Die Tacoma Narrows Bridge aber
geriet durch ihr geringes
Eigengewicht (sie war nur für wenig
Verkehr gebaut worden) und ihre
Schlankheit ganz besonders leicht
ins Schlingern. |
 Am
7. November 1940 kam ein mäßiger
Wind mit einer Geschwindigkeit von
68 km/h auf, der die Brücke erneut
in leichte Schwingungen mit einer
Frequenz von etwa 36 Hz und einer
Amplitude von etwa 60cm versetzte.
Anders als sonst wurden diese jedoch
immer größer und führten zu immer
heftigeren Verwindungen des
Fahrdecks. Am
7. November 1940 kam ein mäßiger
Wind mit einer Geschwindigkeit von
68 km/h auf, der die Brücke erneut
in leichte Schwingungen mit einer
Frequenz von etwa 36 Hz und einer
Amplitude von etwa 60cm versetzte.
Anders als sonst wurden diese jedoch
immer größer und führten zu immer
heftigeren Verwindungen des
Fahrdecks. |
|
 Später
ergab sich eine Rotationsschwingung
mit einer Frequenz von etwa 14 Hz.
Diese neue Schwingung brachte die
Brücke zum Einsturz. Wissenschaftler
des California Institute of
Technology fanden den Grund
schließlich mit Hilfe von Messungen
im Windkanal. Später
ergab sich eine Rotationsschwingung
mit einer Frequenz von etwa 14 Hz.
Diese neue Schwingung brachte die
Brücke zum Einsturz. Wissenschaftler
des California Institute of
Technology fanden den Grund
schließlich mit Hilfe von Messungen
im Windkanal. |
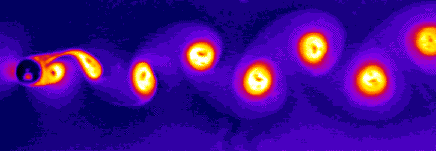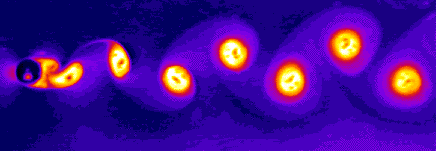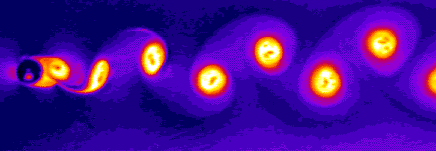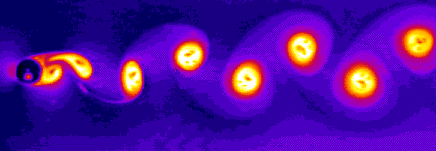 Es
war eine durch die Form des
Strömungsprofils der Brücke
hervorgerufene Wirbelbildung des
Windes, welche die Brücke in ihrer
Eigenfrequenz (Resonanz) anregte.
Seit dieser Katastrophe darf keine
Brücke mehr ohne entsprechende
Windkanaltests gebaut werden. Es
war eine durch die Form des
Strömungsprofils der Brücke
hervorgerufene Wirbelbildung des
Windes, welche die Brücke in ihrer
Eigenfrequenz (Resonanz) anregte.
Seit dieser Katastrophe darf keine
Brücke mehr ohne entsprechende
Windkanaltests gebaut werden. |
|
|
|
|
letzte Änderung: 8.5.2005 |



















